上午题-3-数据结构
[toc]
复杂度
大O表示法

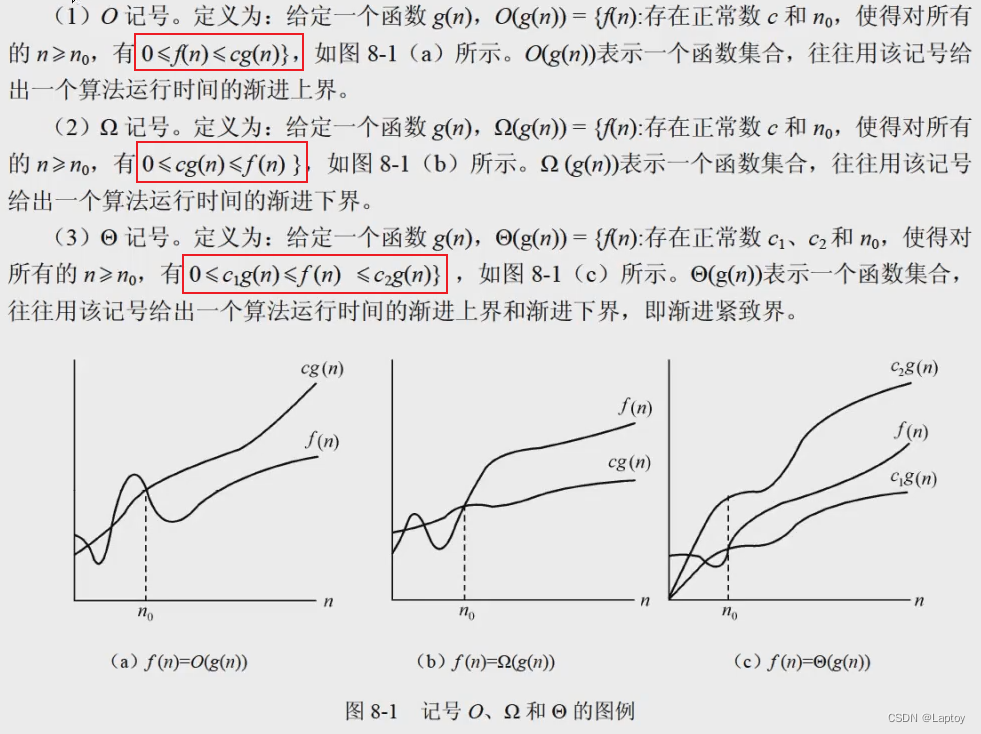
渐进符号
例题

由渐进上界的定义,0<=f(n)<=cg(n)
则f(n)=O(g(n))
递归 主方法


线性结构
线性表
- 顺序存储——一组地址连续的存储单元
- 链式存储——地址不要是连续的
链式存储
头结点:在首元结点之前附设的一个结点,其指针指向首元结点
首元结点:指链表中存储第一个元素的结点
头指针:指向链表中的第一个结点,若有头结点,则指向头结点,否则指向首元结点。
插入的时间复杂度
最好情况是O(1),插入第一个结点后面一个结点的位置
最坏情况是O(n),插入在最后面(因为要让链表遍历到尾,p=p->next)
平均时间复杂度是O(n)
删除、查找也是类似,最好是O(1),最坏是O(n),平均是O(n)
题目

插入是直接在尾指针后面插
删除由于要找到位置在前面的结点,所以是O(n)
循环链表的特点是表中最后一个结点的指针域指向头结点
栈
后进先出
队列
先进先出
串


计算next的例子

- 算i=5,即a的next数组,即要计算1~4串中,最长相等前后缀长度+1
- 先让前后缀长度为1,则前缀为a,后缀为b,不相等,所以为0
- 再让前后缀长度为2,前缀为ab,后缀为ab,相等,所以为2
- 再让前后缀长度为3,前缀为aba,后缀为bab,不相等,所以为0
- 不能为4,因为前缀不能包含最后一个字符,后缀不能包含第一个字符。
- 所以next[5]=2+1=3
矩阵

树
概念
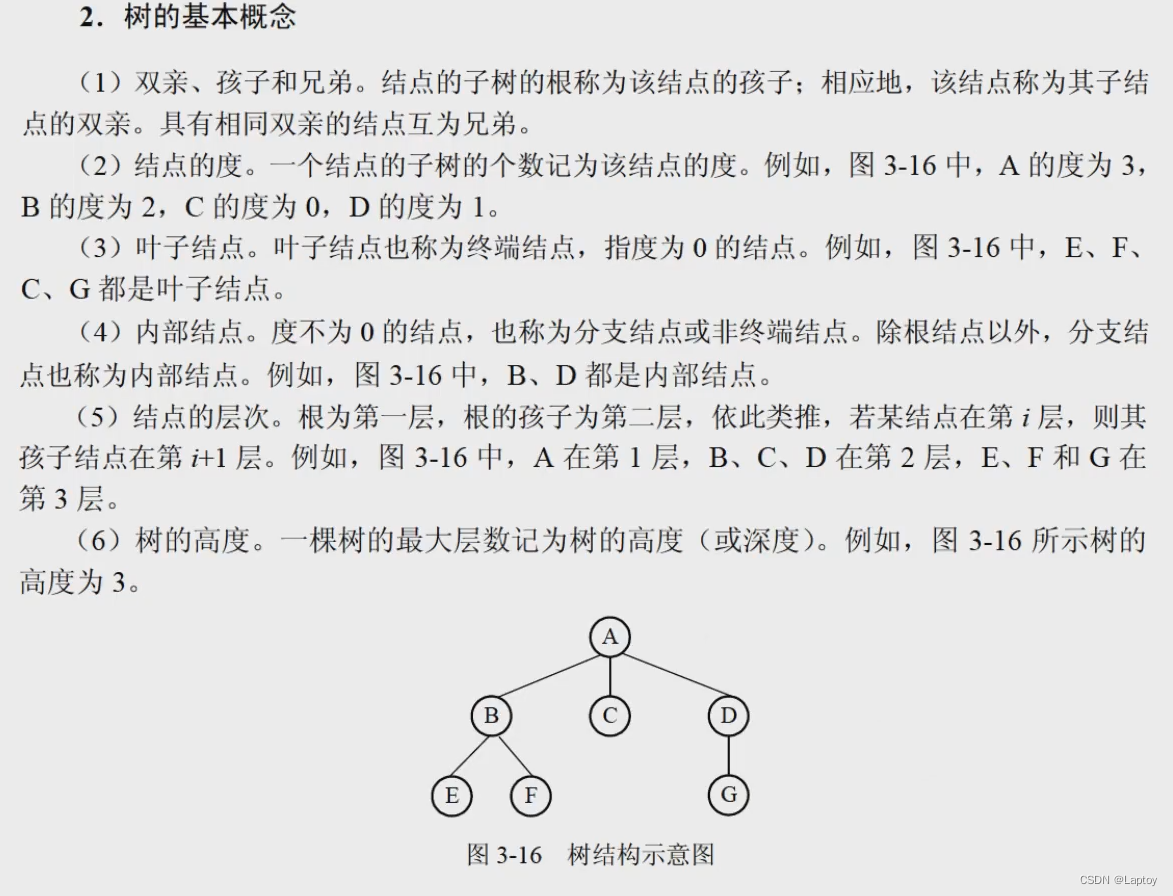
- 度
性质
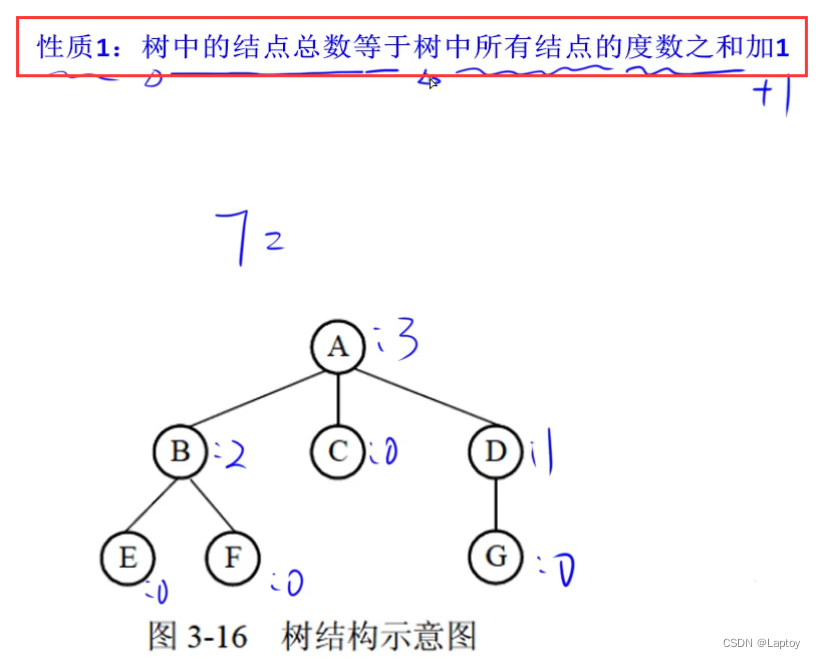
很好理解,度是每个结点的子结点数,加个1是根结点。

度为m的意思应该是结点的度要么为m要么为0(叶子结点)
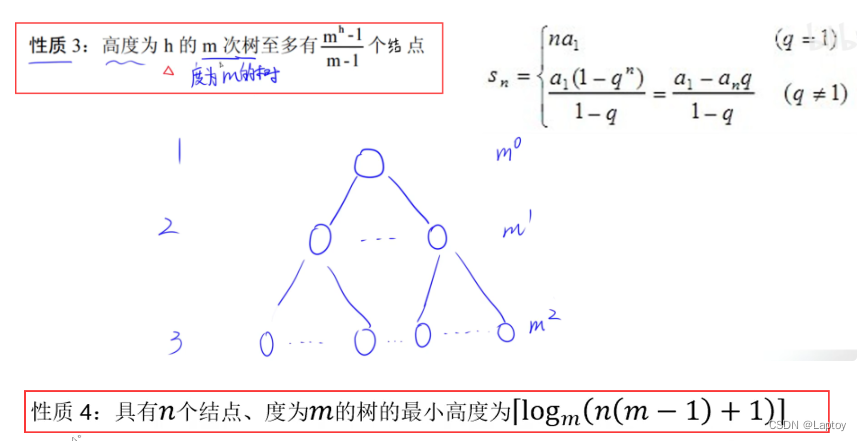
度为2的树,高度为3,最多有(2^3-1)/(2-1)=7个结点(1、2、4)
度为3的树,高度为3,最多有(3^3-1)/(3-1)=13个结点(1、3、9)
二叉树

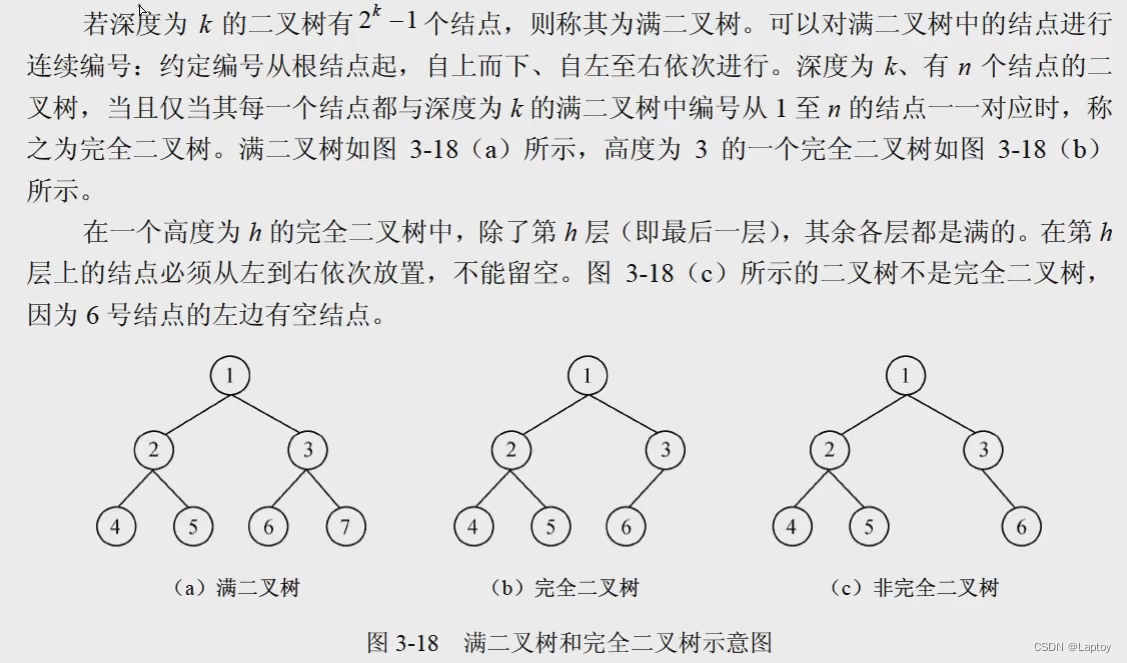
满二叉树和完全二叉树
存储结构
顺序存储

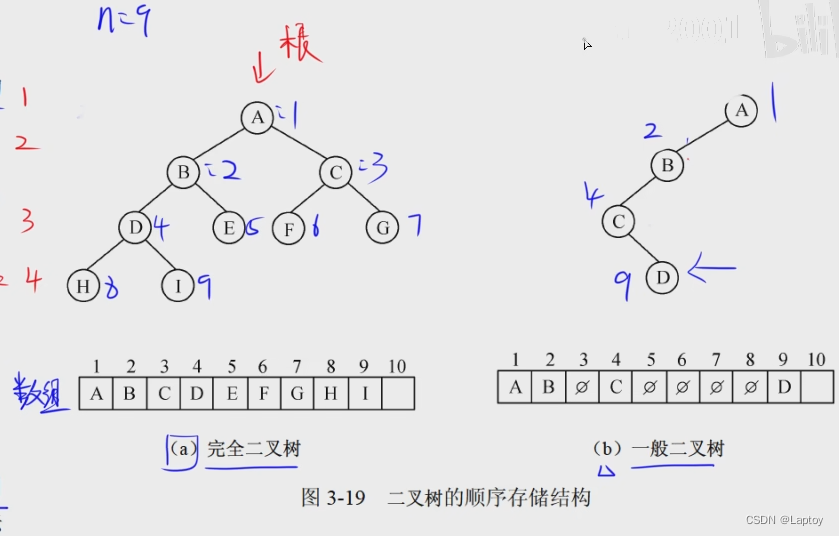
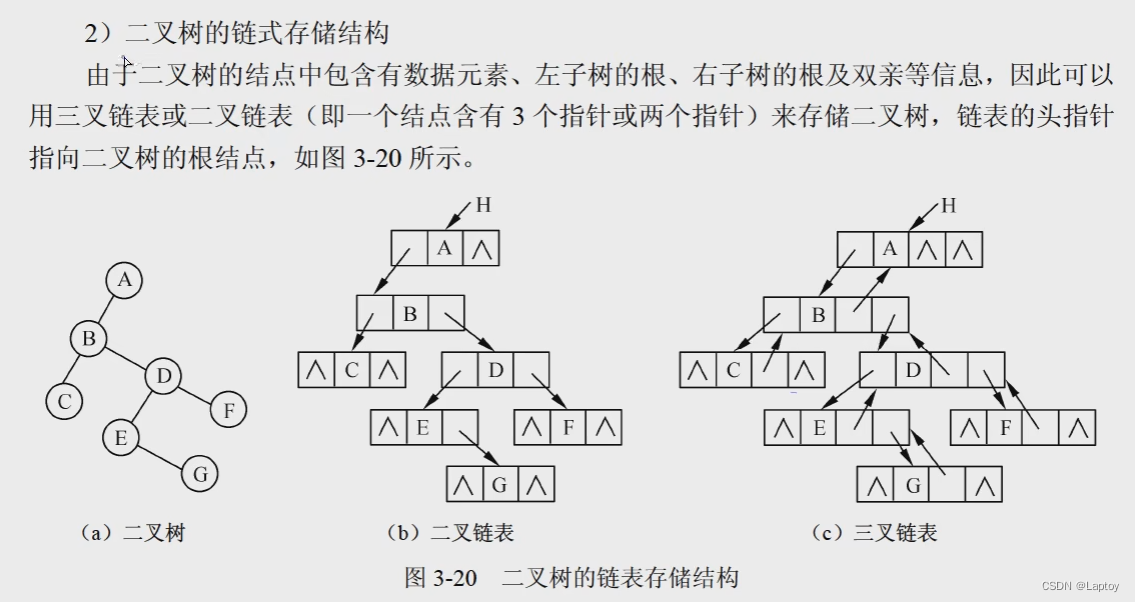

对于二叉链表来说,n个结点除去根结点的话,就有n-1个结点被指,所以n-1个指针不为空。
对于三叉链表来说,n个结点除去根结点的话,就有n-1个结点被指,以及n-1个结点的父指针有效,所以2n-2个指针不为空。
遍历
- 先序遍历,根左右
- 中序遍历,左根右
- 后序遍历,左右根
- 层次遍历
- 访问根结点
- 从左到右访问第二层所有节点
- ...
反向构造
由一种遍历序列构造的二叉树可能不唯一。
但是如果还知道了中序序列加上先序、后序、层次遍历序列的任意一种,那么就可以构造出一颗唯一的二叉树。(因为这三种遍历方式根结点都是在第一的)
平衡二叉树

二叉排序树
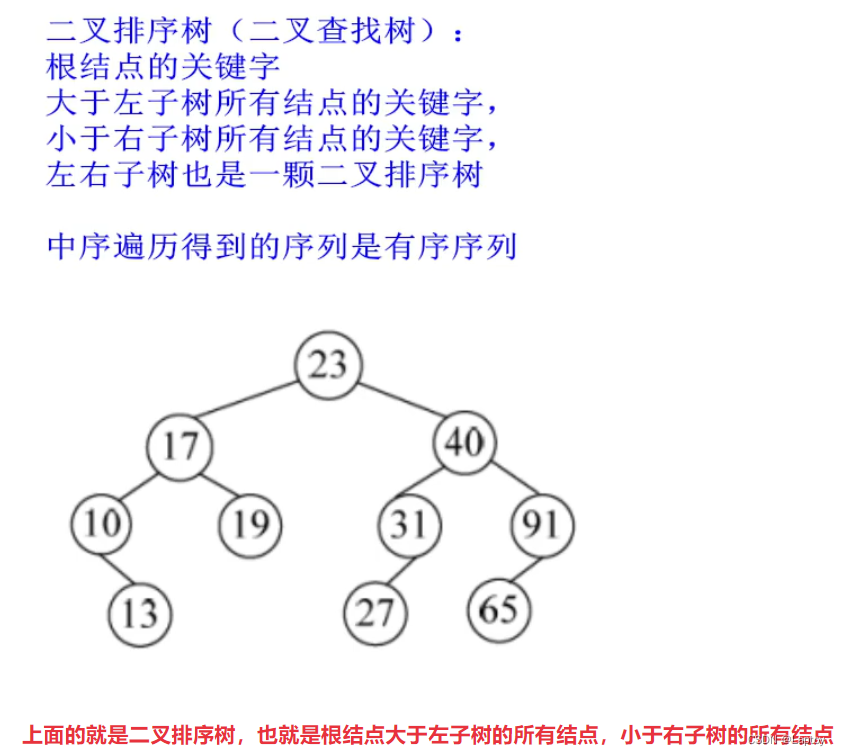
最优二叉树(哈夫曼数)

构造哈夫曼树
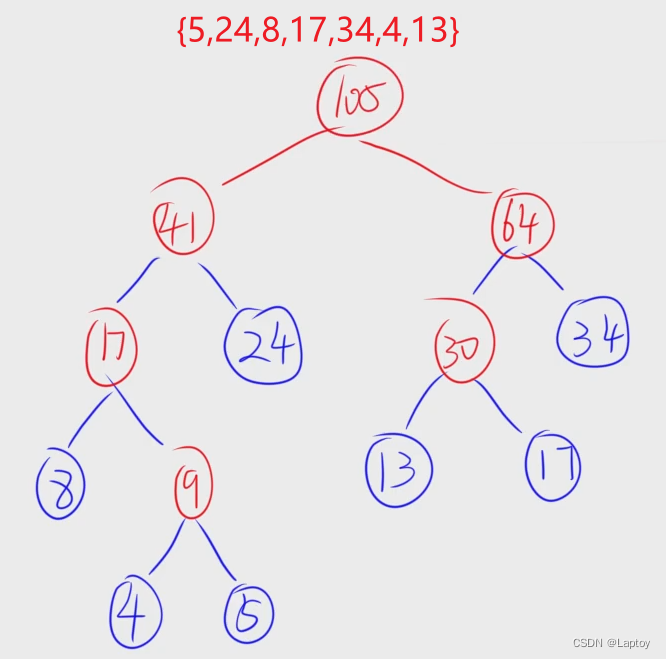
哈夫曼树的总结点数是2n-1(n是叶子节点数)
哈夫曼编码
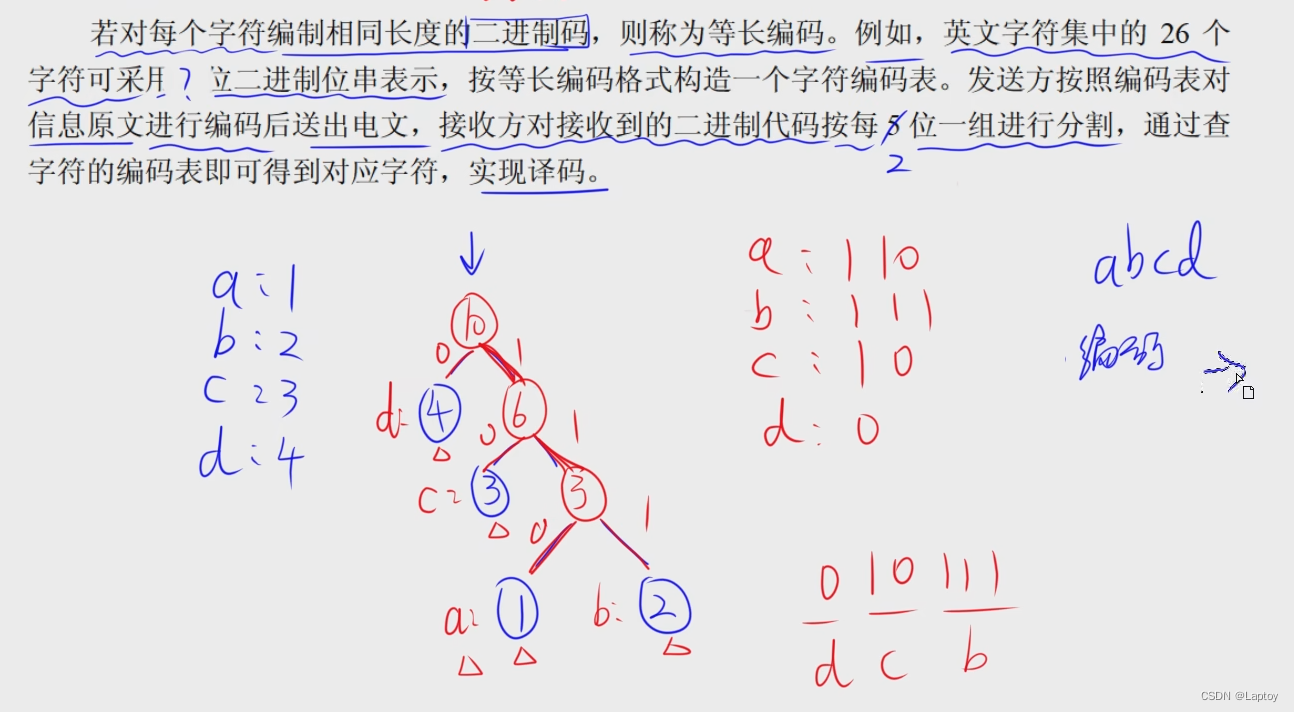
计算压缩比
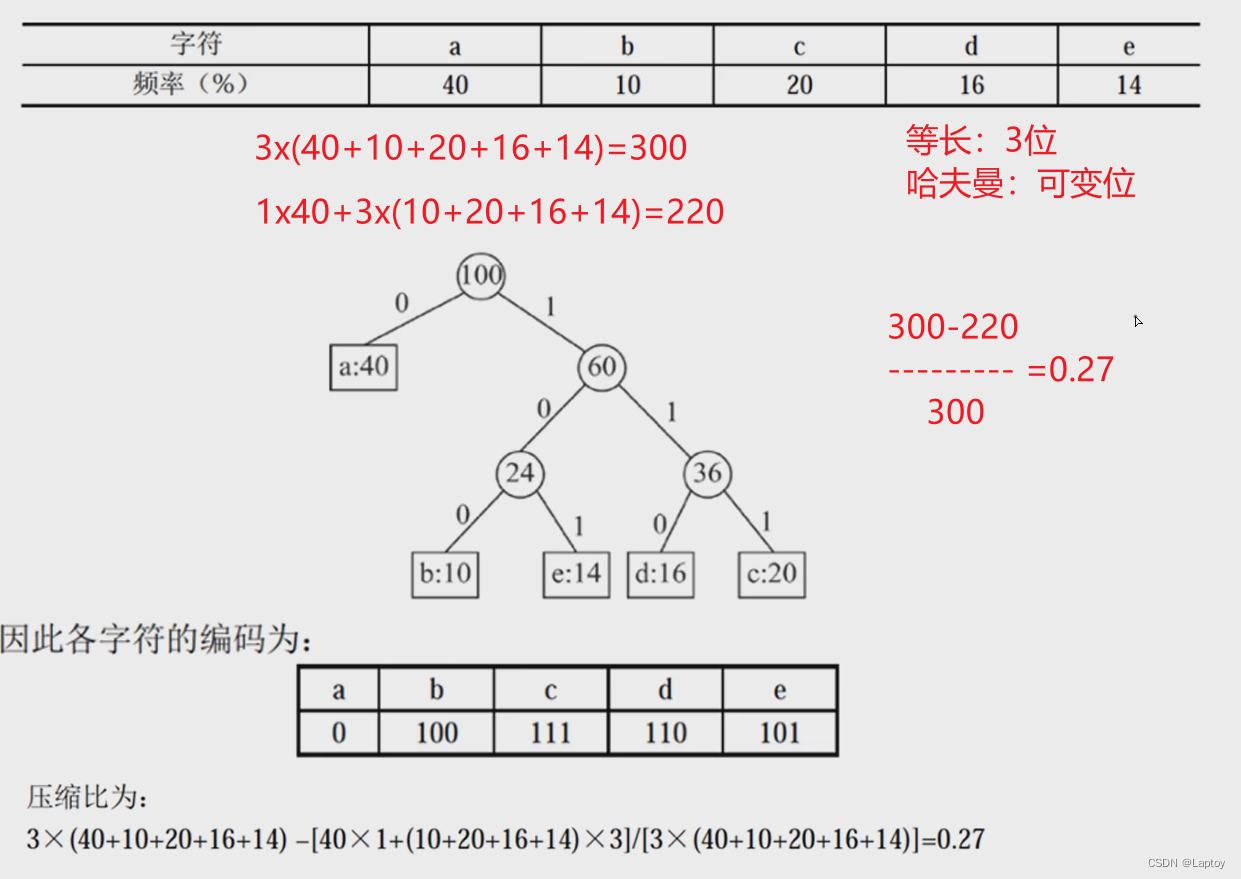
原本5个字符最少要用3位表示,2^3>5
5个字符最少需要3位二位进数表示,即每个字符用三位表示
通过哈夫曼树优化后,a用0表示,只有1位
- 按照出现频率计算加权平均长度:字符位数 * 出现频率
a的位数 * 40% + b的位数 * 10% + c的位数 * 20% + d的位数 * 16% + e的位数 * 14%
= 1 * 40% + 3 * 10% + 3 * 20% + 3 * 16% + 3 * 14%
= 2.2位
- 计算压缩比
未压缩长度为 3 ,压缩后平均长度为 2.2
(3 - 2.2)/3 = 27%
线索二叉树
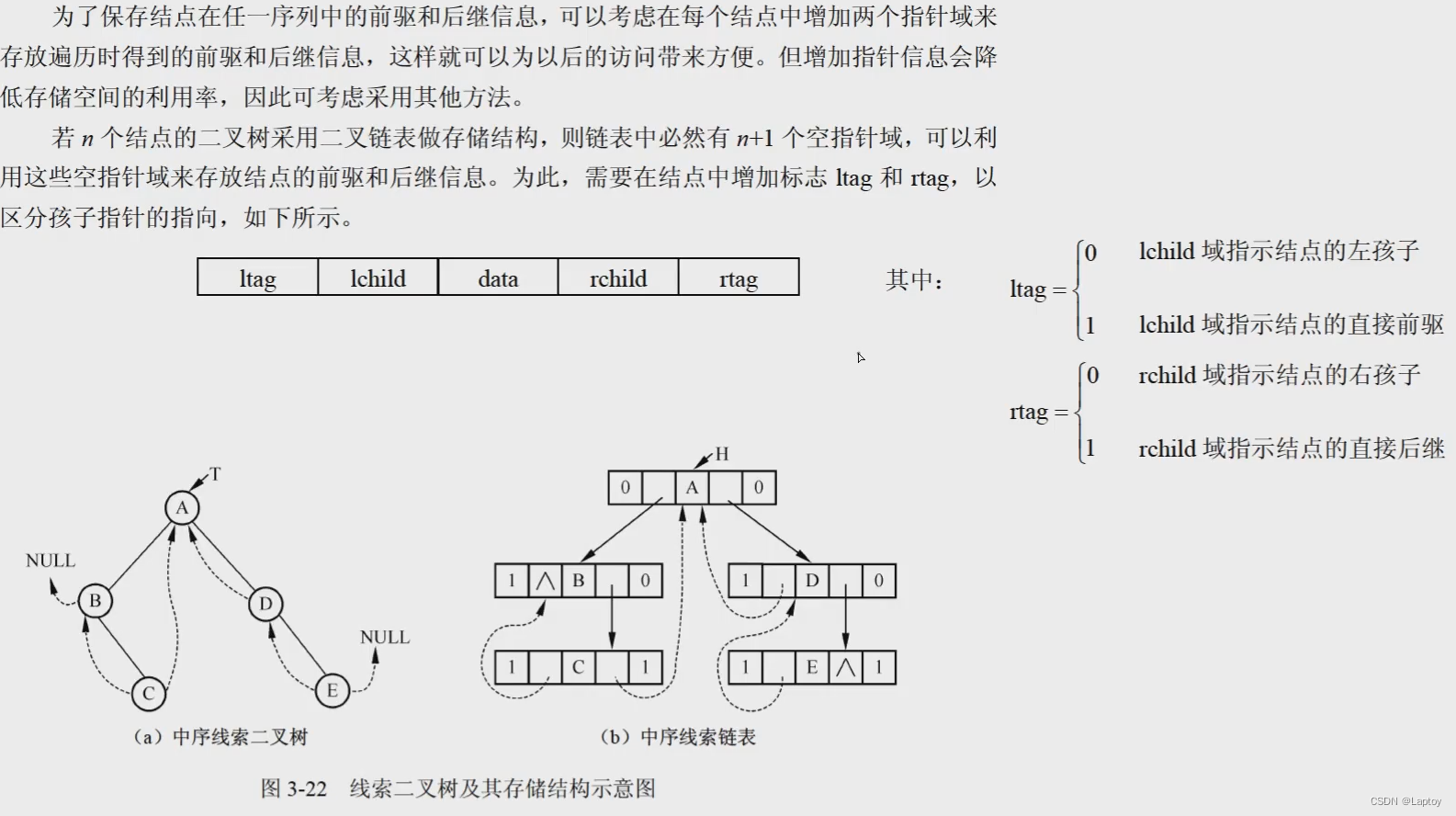
图
概念
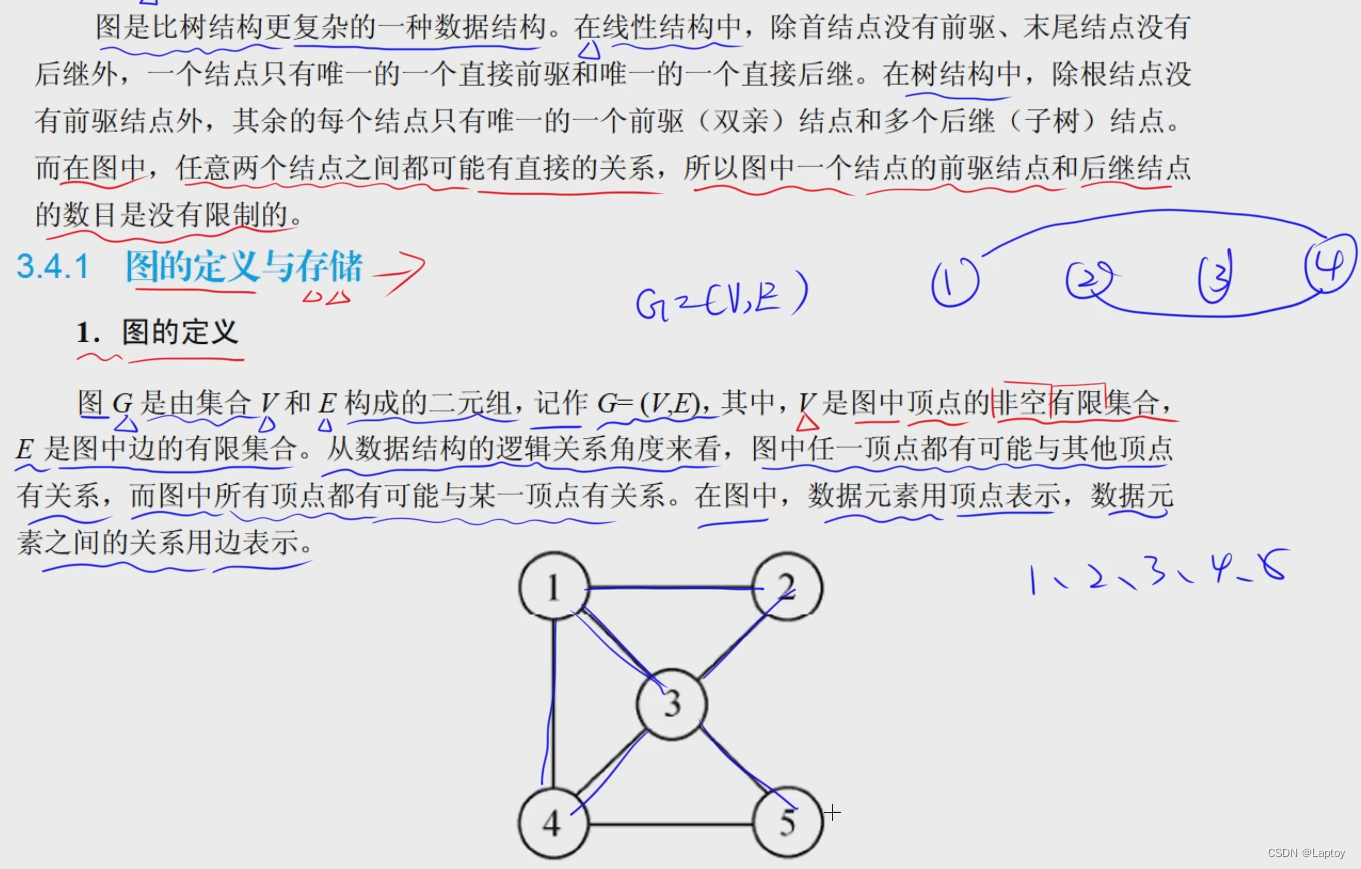
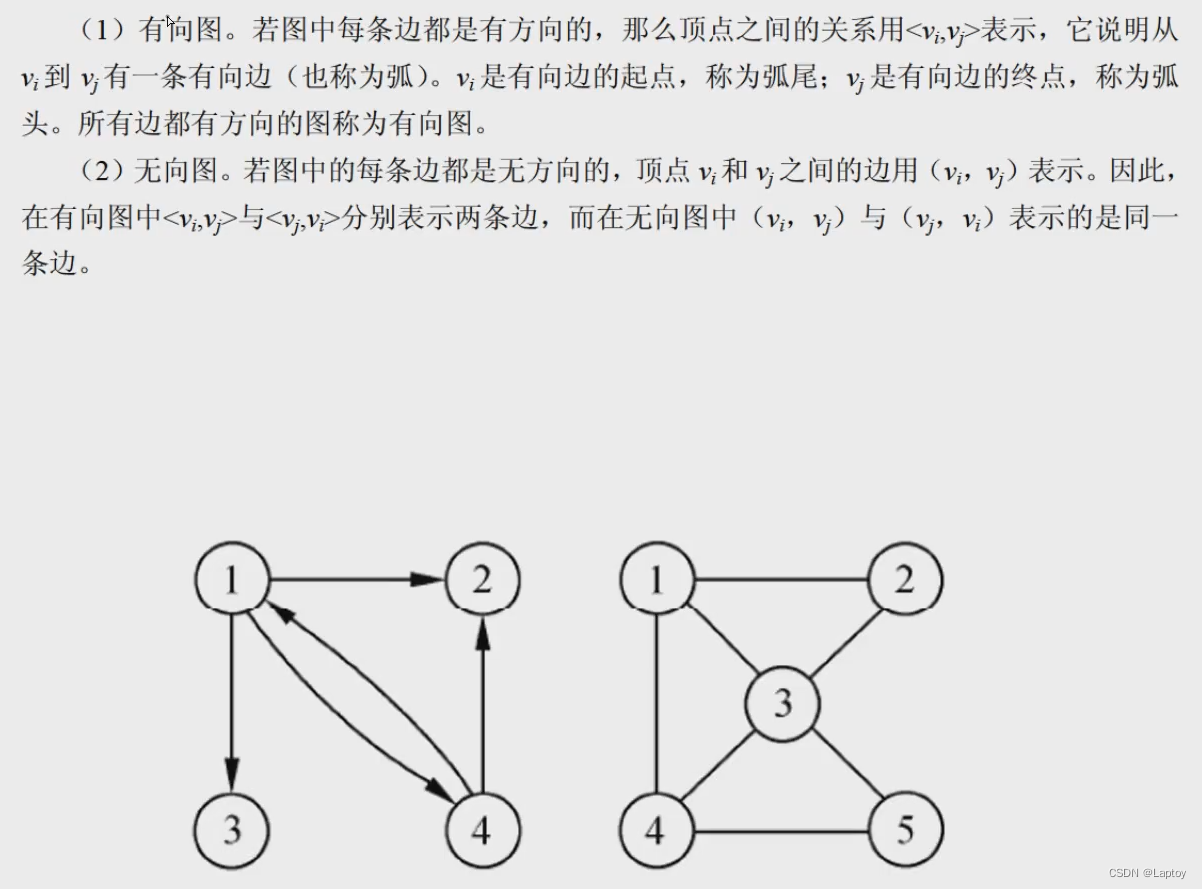

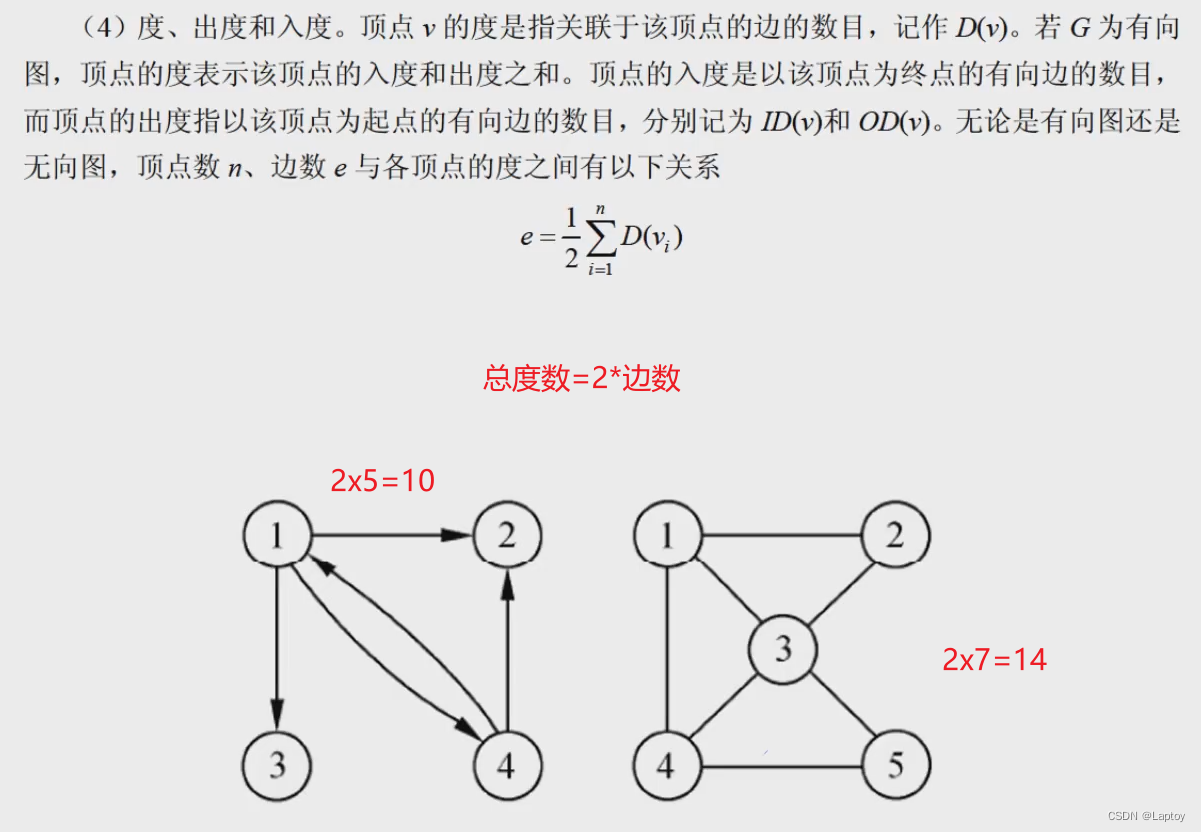
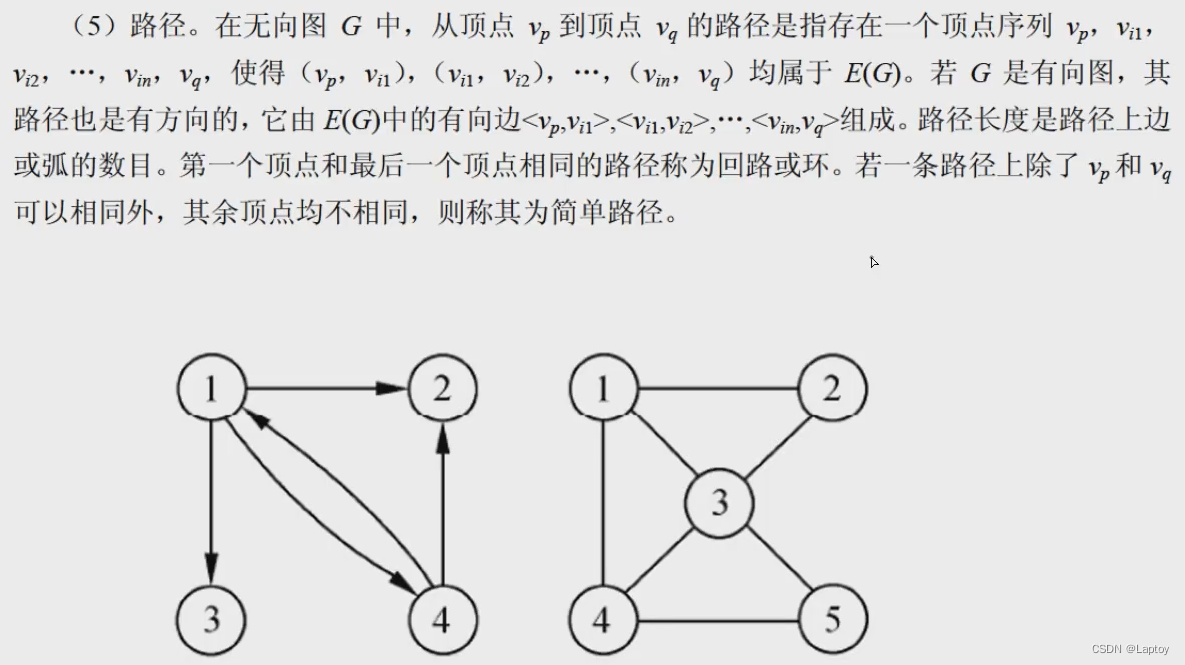
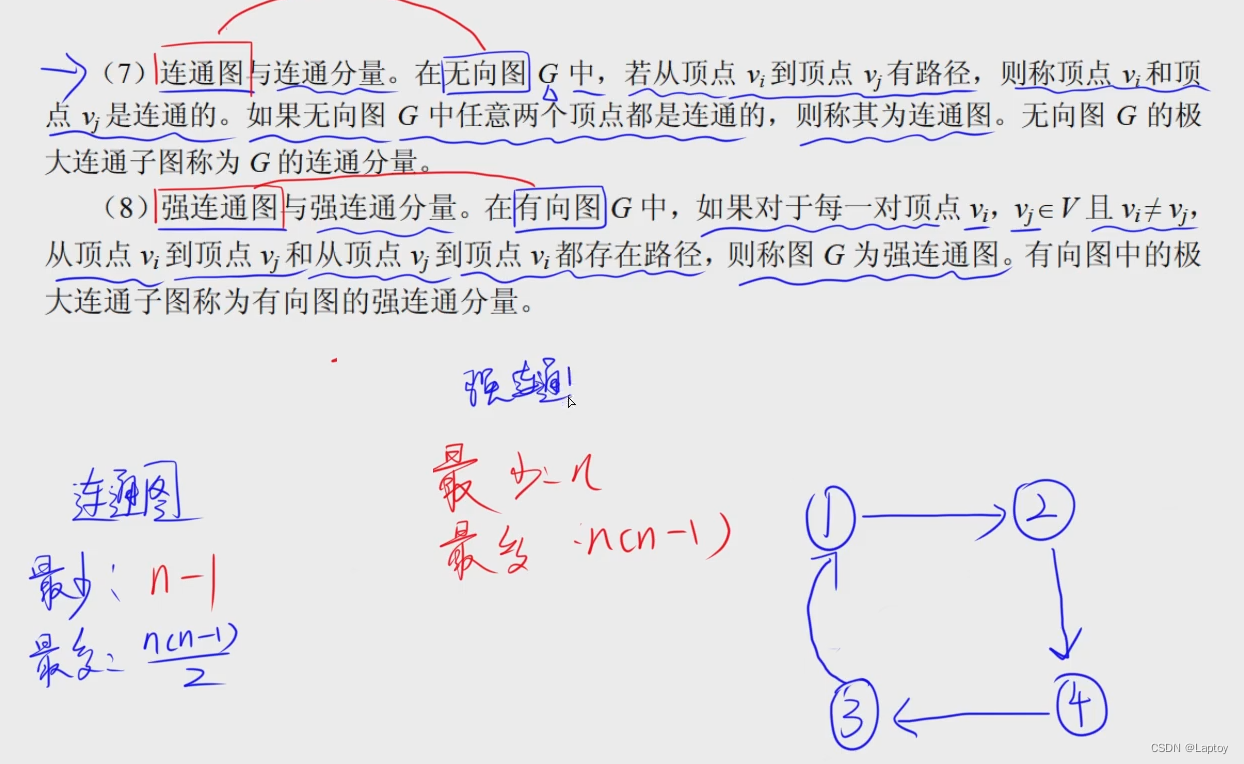
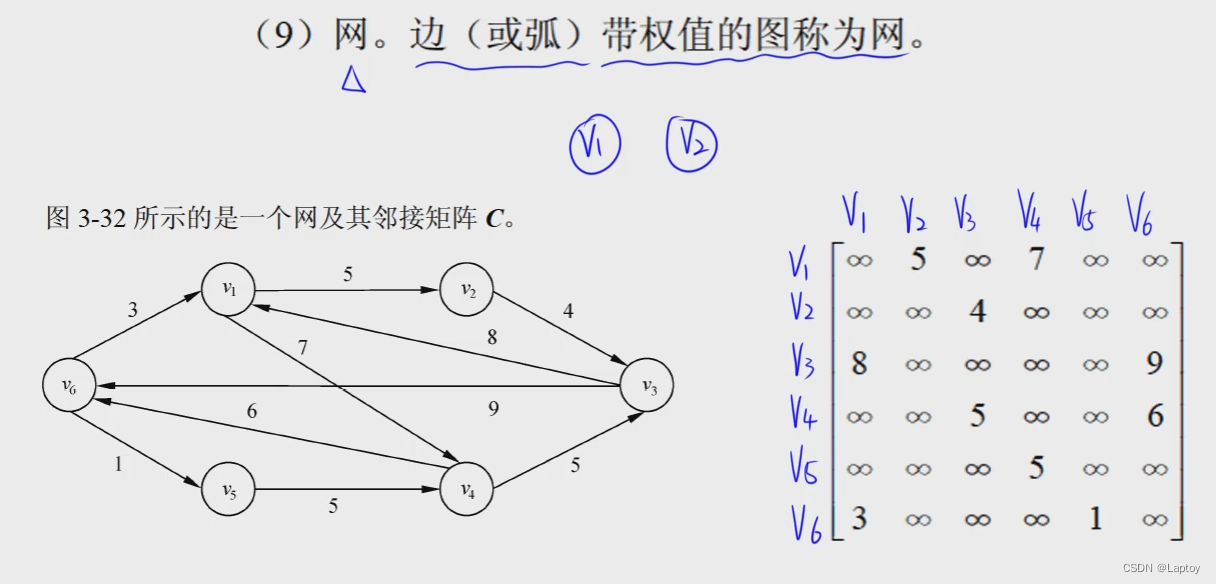
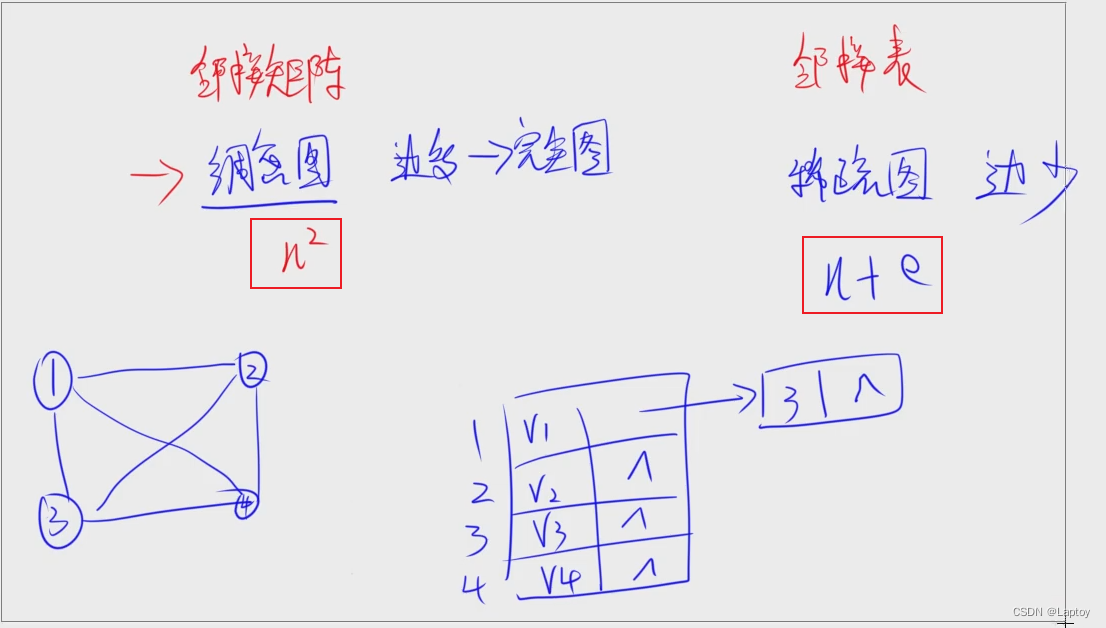
邻接矩阵

邻接表
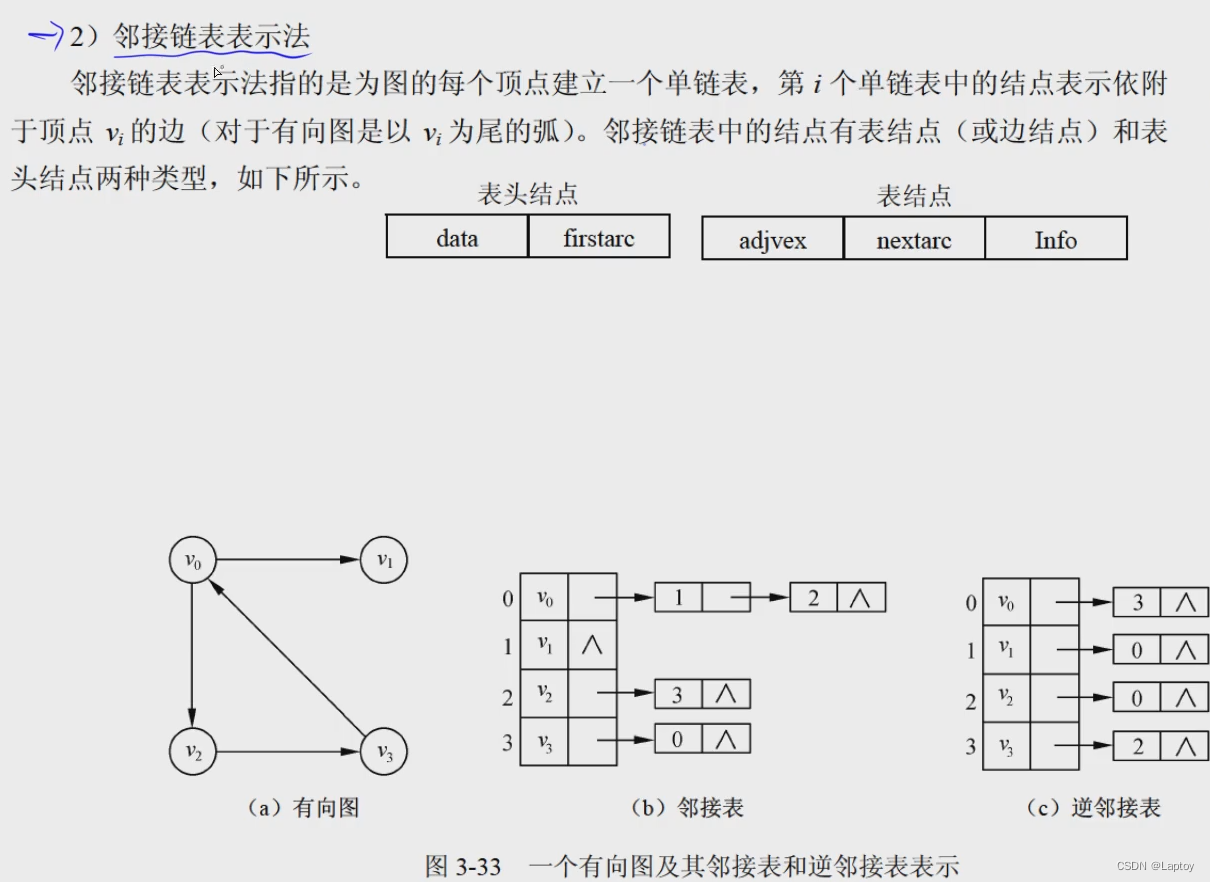
稠密图和稀疏图
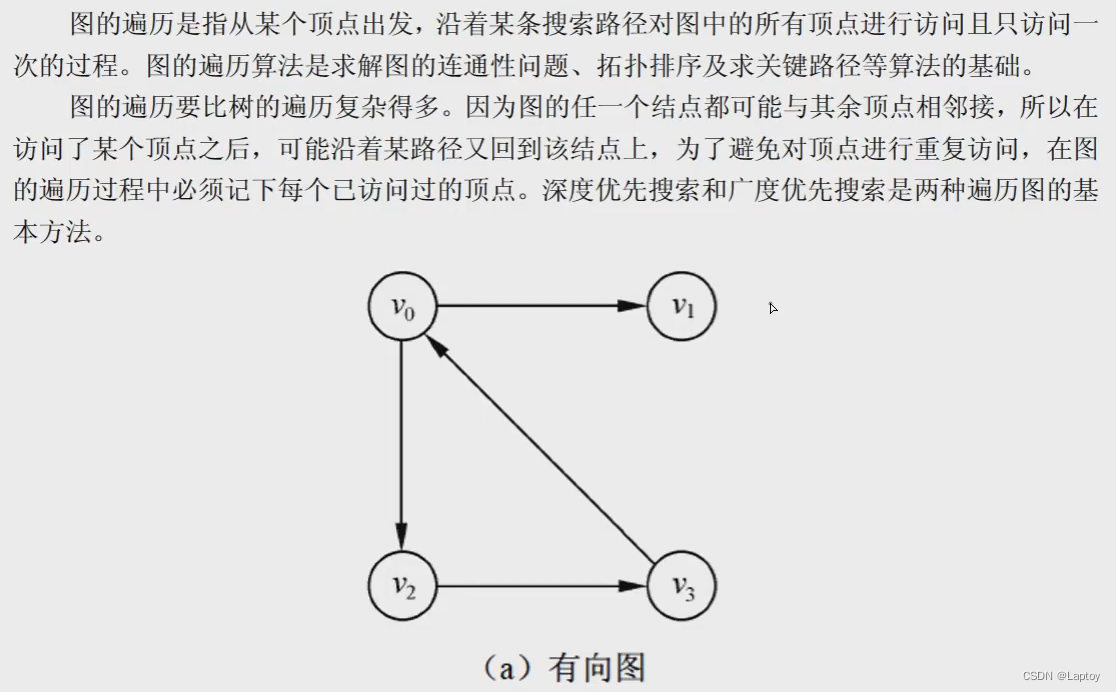
图的遍历
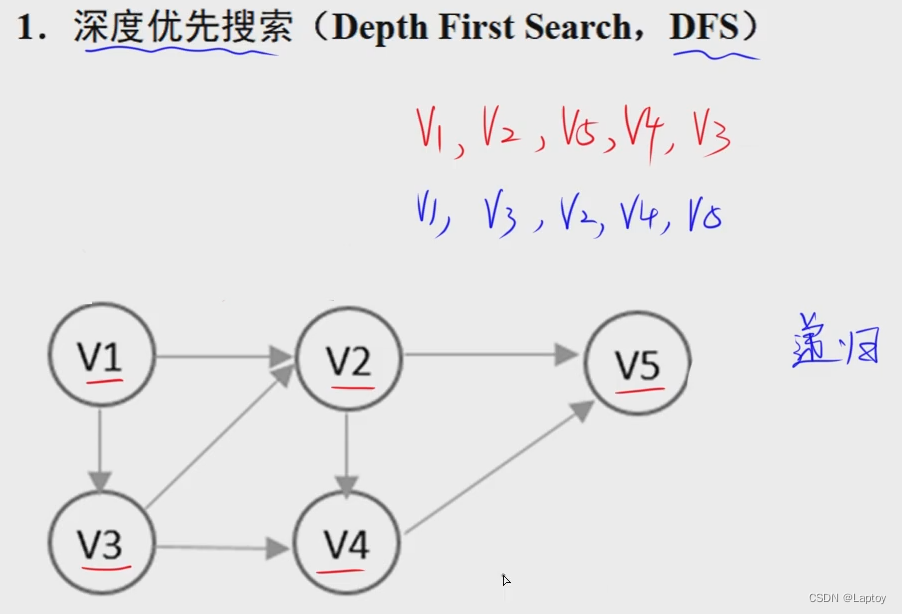
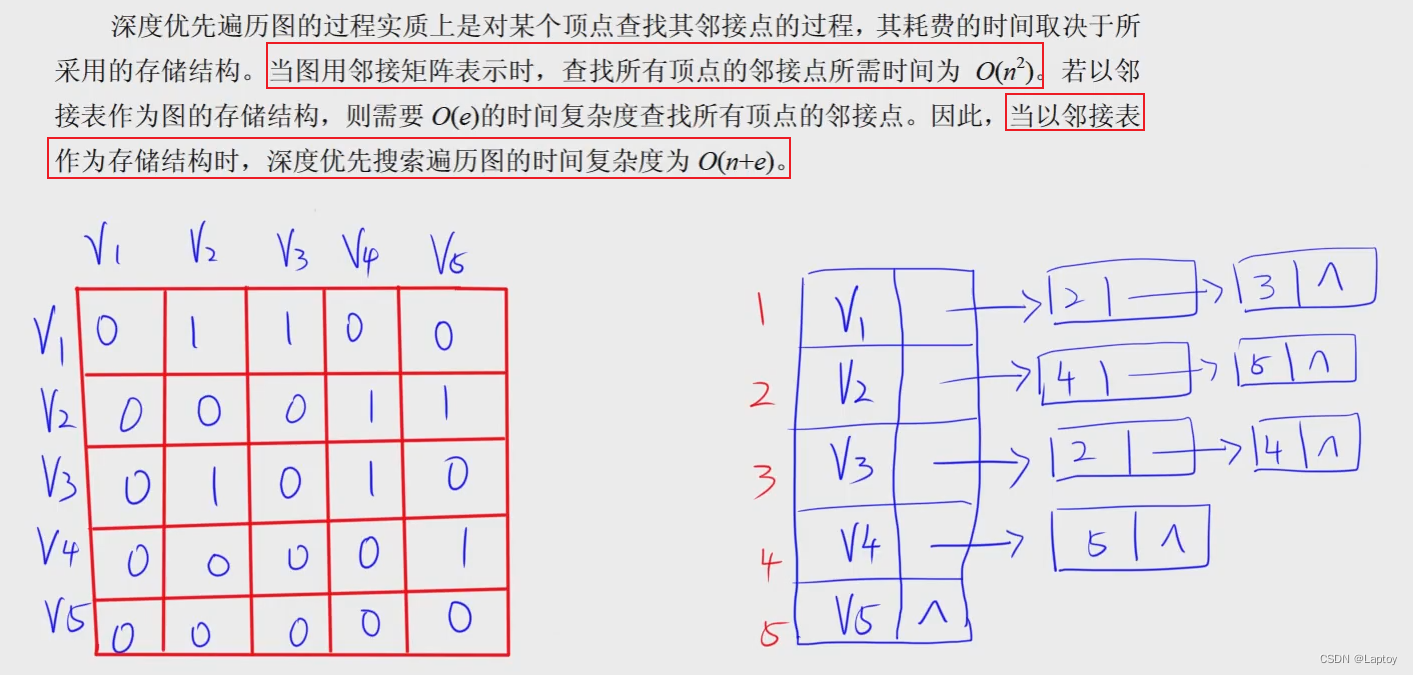
DFS
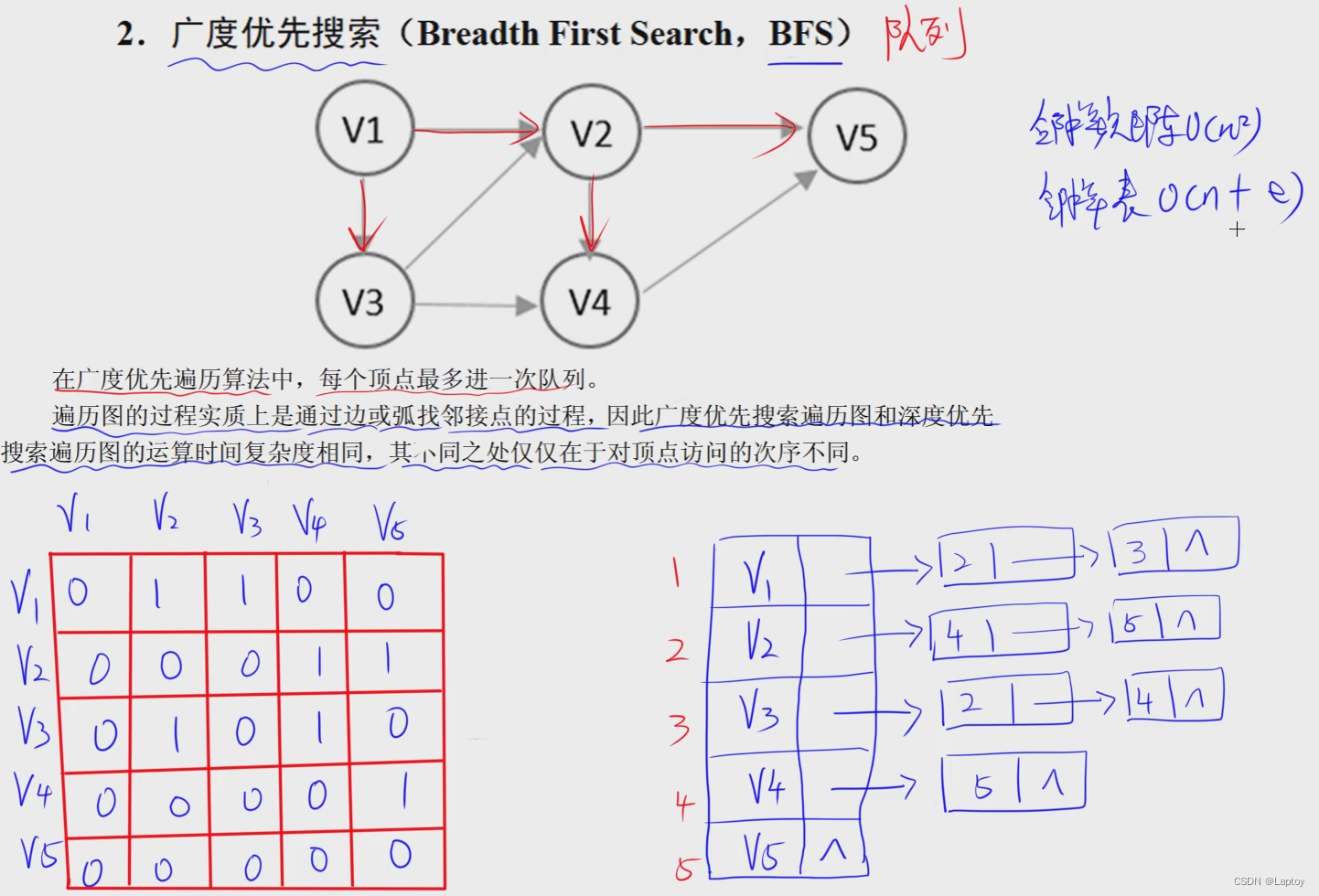
BFS
拓扑排序



查找
概念



顺序查找

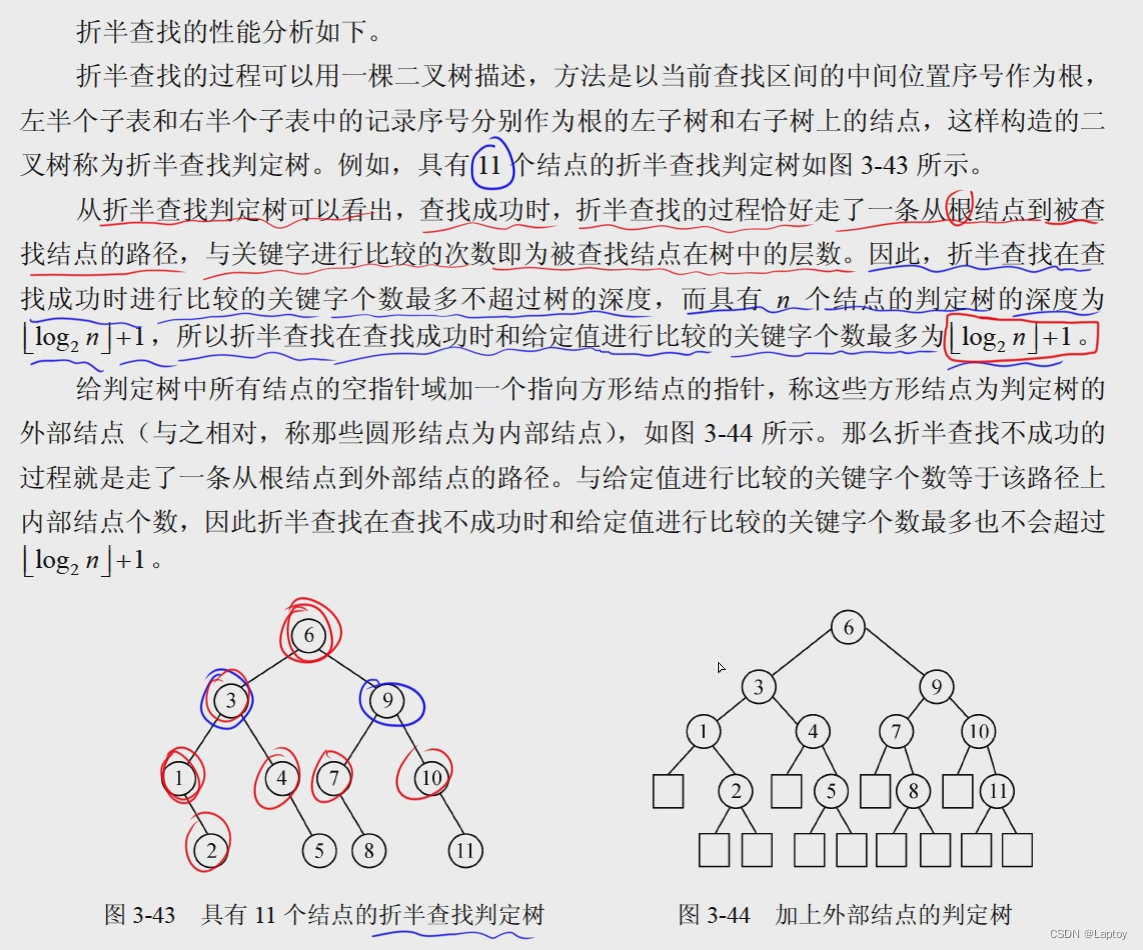
二分查找

哈希表
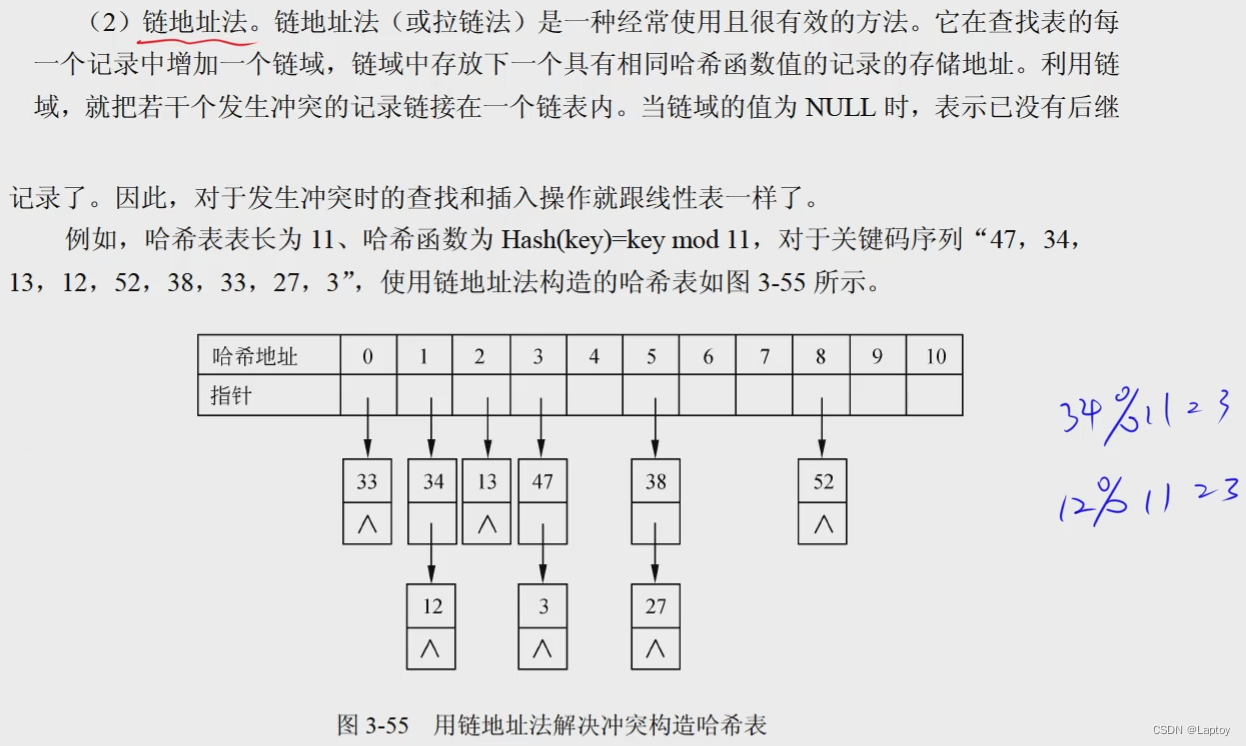
哈希函数构造与处理冲突

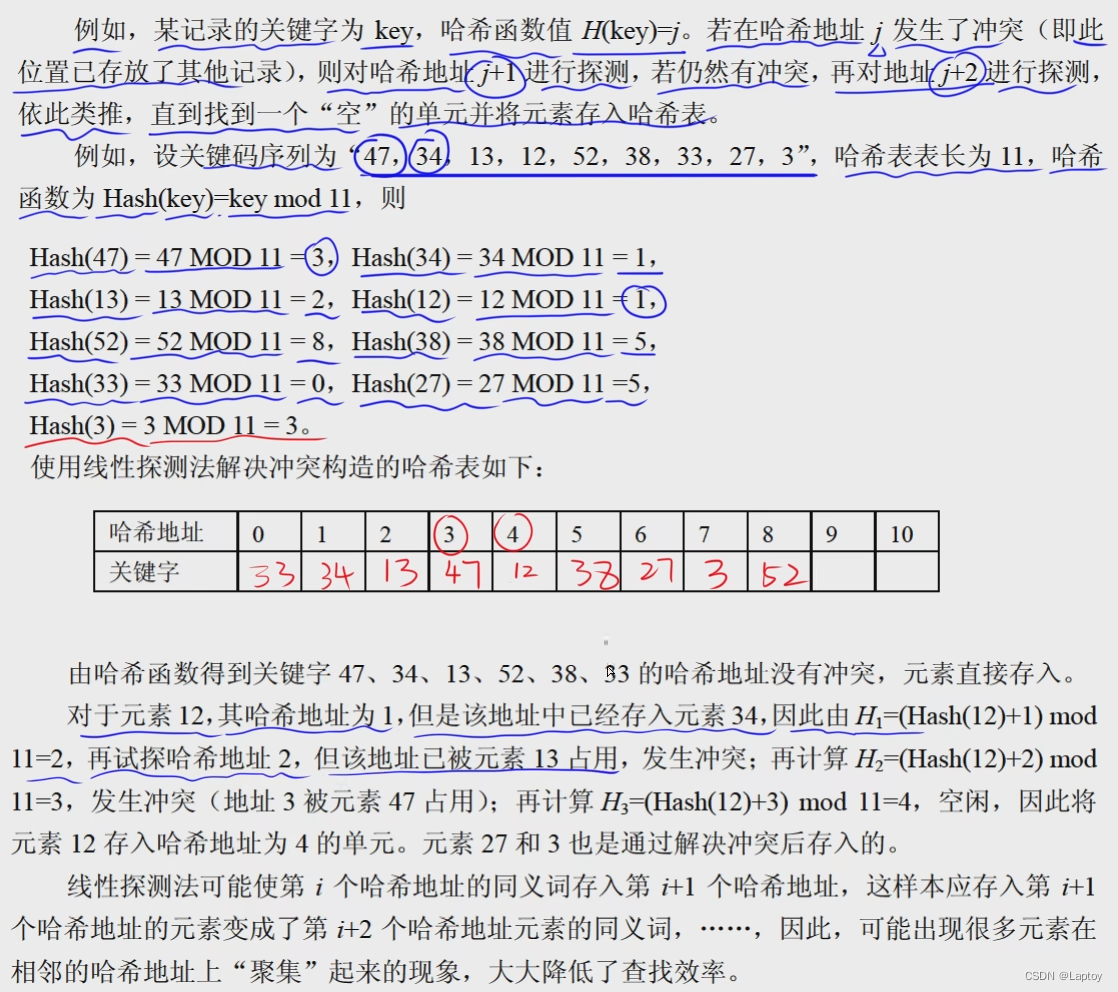
常见的增量序列:
- 线性探测再散列
- 二次探测再散列
- 随机探测再散列

堆
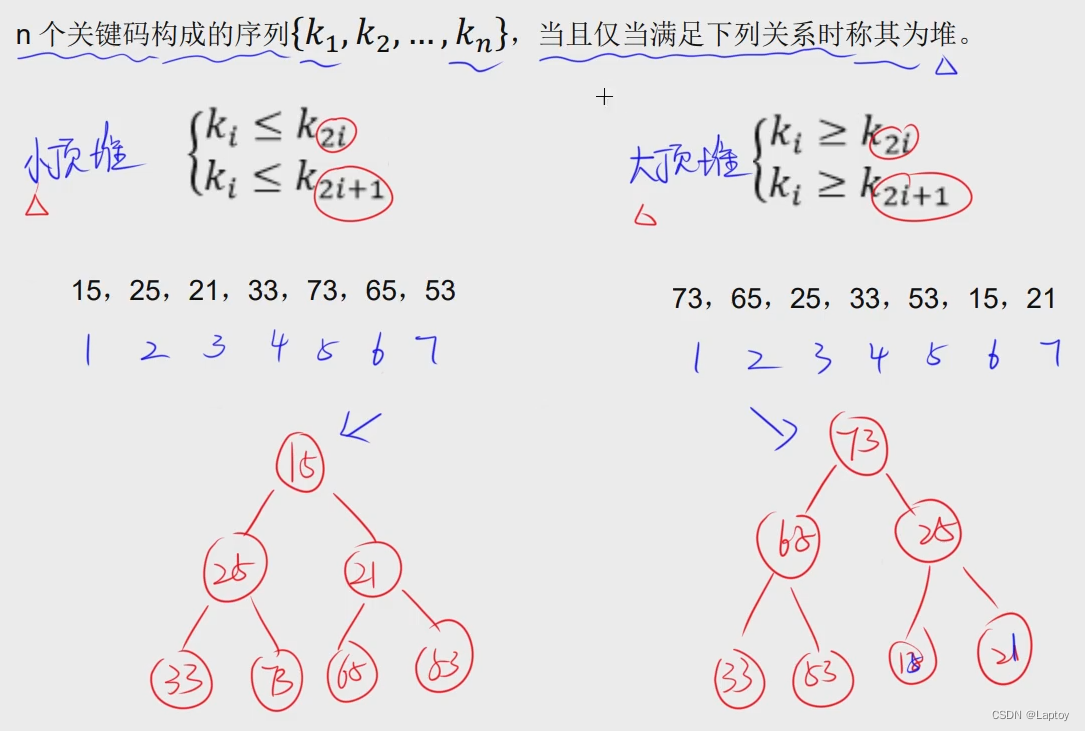
建立大根堆和小根堆(或大顶堆,小顶堆)
- 先由序列建立二叉树,按顺序,每层都是满的(1、2、4...),最后一层不要求满
- 然后从底部开始调整,如果父结点大于两个子结点,不需要交换。
- 如果父结点小于其中一个子结点,则将他们进行交换。
- 如果父结点小于两个子结点,则将它与较大的子结点交换。
- 如果交换后,不满足大根堆的性质,继续重复。
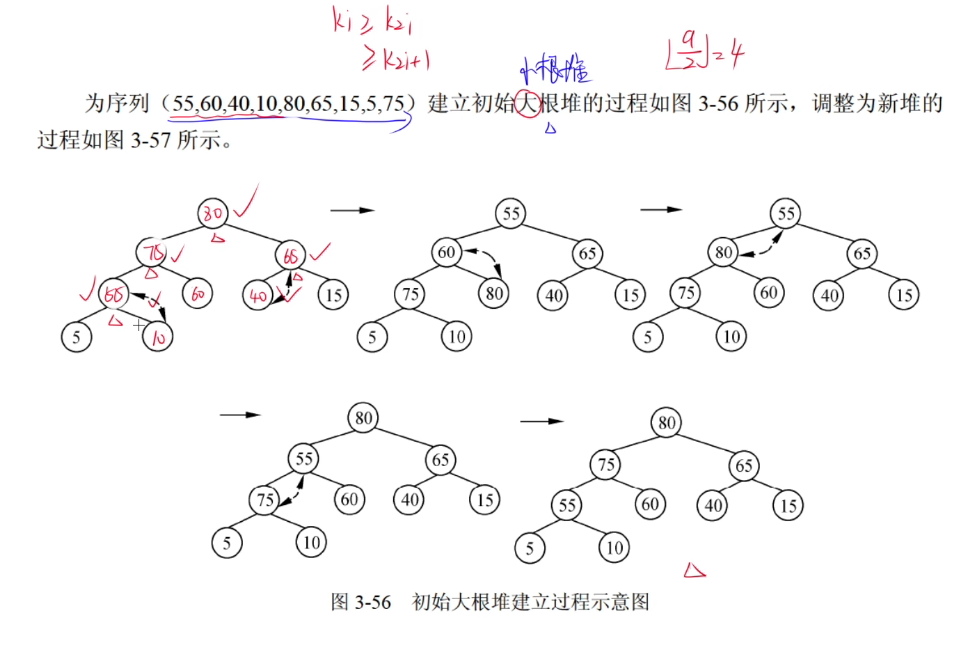
排序

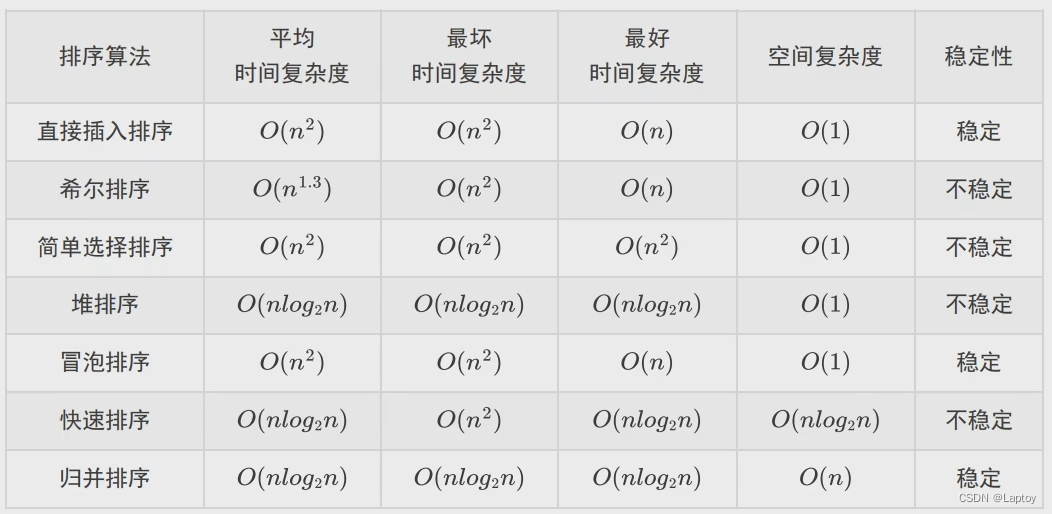
稳定的排序只有:
- 直接插入排序
- 冒泡排序
- 归并排序
插入排序
适用于序列基本上有序
将一个待排序的数组分成两部分,前一部分代表是有序序列,后一部分代表未排序序列
将第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列
从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置
如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面,直到未排序序列全部扫描完毕为止
无法归位(元素位置在下一轮可能改变)

希尔排序

选择排序
- 从待排序的元素中选出最小的元素,存放在起始位置,固定住该最小元素
- 同理取出未固定的元素中的最小元素,存放在起始位置,固定
- 以此类推,直到全部待排序的数据元素的个数为零。
- 5个元素只需要选择4次,因为最后一个默认为最大的

堆排序
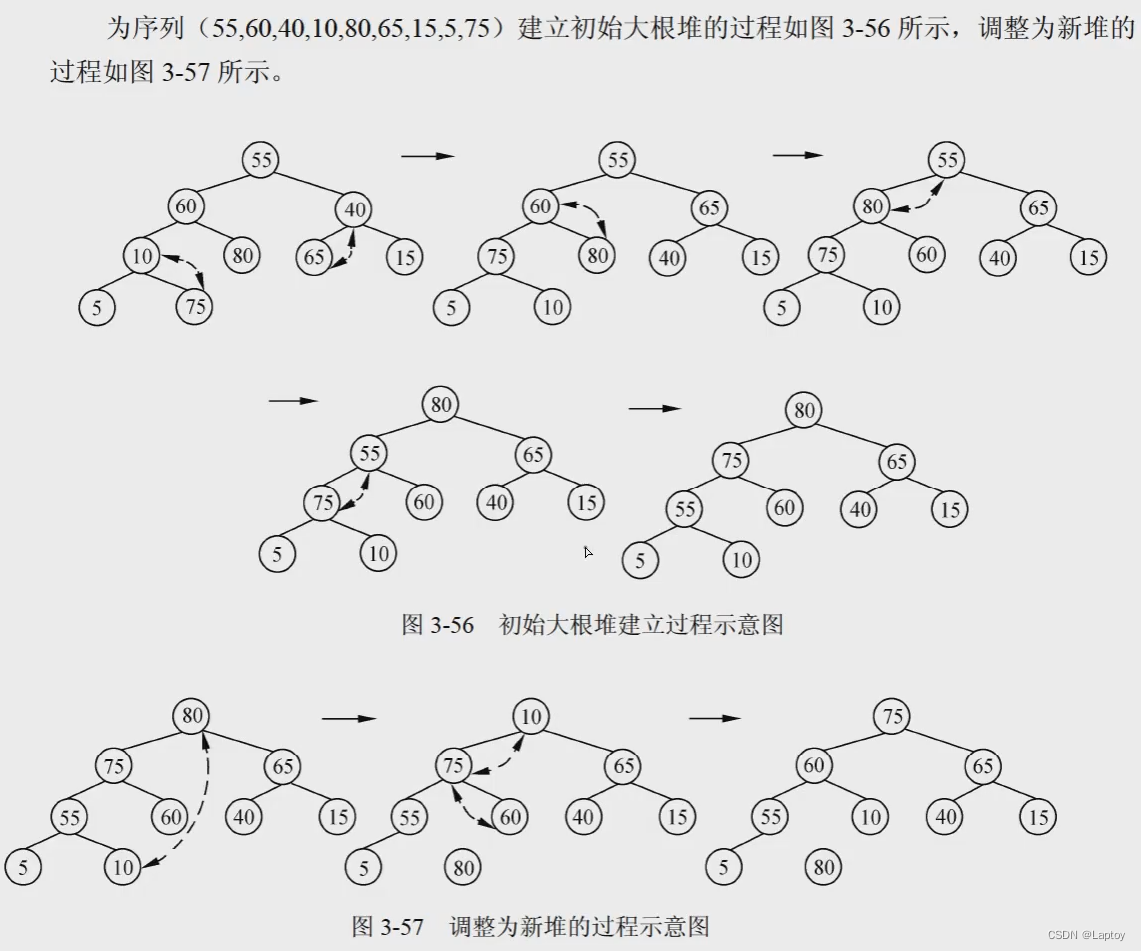
冒泡排序
- 比较相邻的元素,如果第一个比第二个大,就交换他们两个
- 对每一对相邻元素做同样的工作,从开始的第一对到结尾的最后一对,这步做完后,最后的元素应该会是最大的数
- 每次过后,需要排序的元素就越来越少,对剩下需要排序的元素重复上面的步骤,直到没有任何一对数字需要比较

快速排序

归并排序